Поговорим о сетках треугольников. Квадратные сетки используются практически везде, от пикселей изображения до расположения домов на квартале. Шестиугольные сетки также довольно распространены, особенно в настольных играх. Однако треугольные сетки (равномерно заполняющие двумерную плоскость равносторонними треугольниками) почему-то не очень популярны. Я сталкивался с утверждениями, что они бесполезны или что у них сложная математика. Но этой статьей я докажу, что оба утверждения ошибочны: расчеты на самом деле проще, чем с шестиугольниками, а у треугольников много преимуществ.
Все расчеты я делал в своем коде на github, но стоит пояснить, как и зачем нужно использовать такие сетки.
Что такое «сетка треугольников»
Когда я говорю о сетке треугольников, я имею в виду тайловую карту, в которой все тайлы представляют собой одинаковые равносторонние треугольники, расположенные в переменных рядах (или столбцах).

Здесь важно то, что у каждой плитки ровно три соседа. Иногда встречаются игры, где рисуется сетка из треугольников, но на самом деле кусочки находятся в углах. Каждый угол соединяется с шестью другими, так что на самом деле это не треугольники, а шестиугольники.
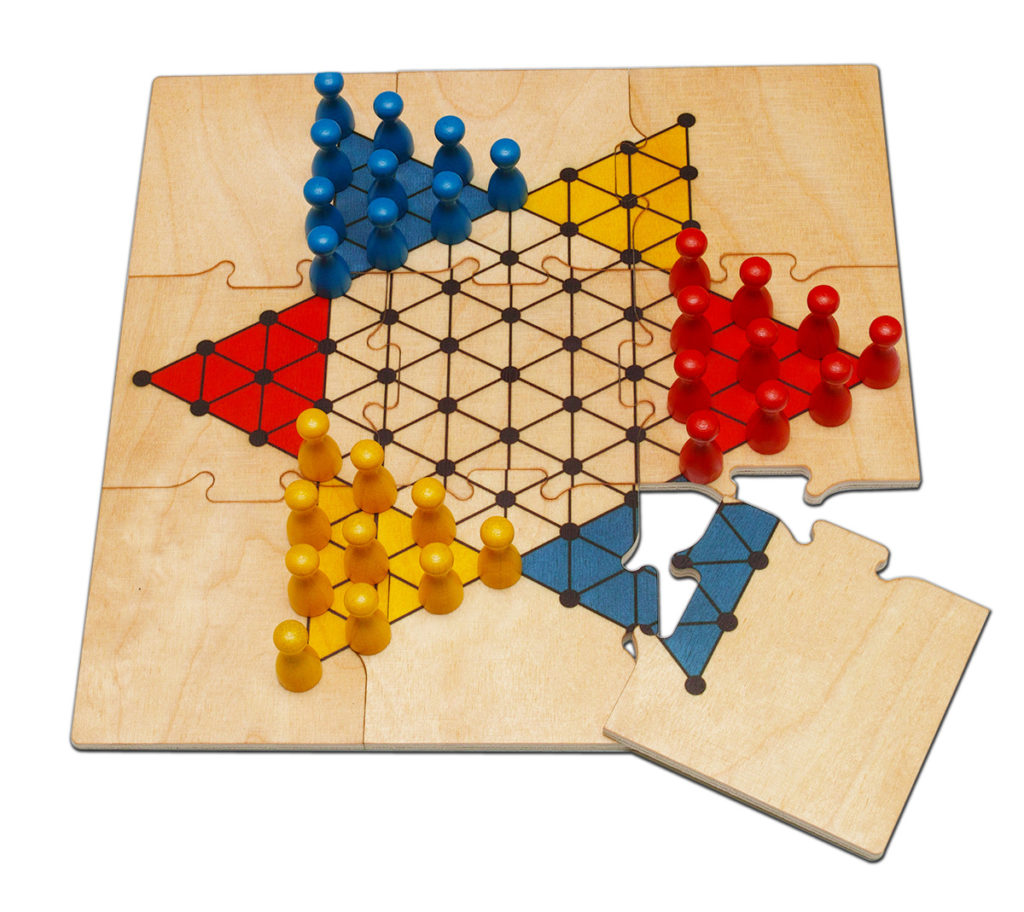
Китайские наркотики (халма) разыгрываются на сетке шестиугольников, стилизованной на рисунке под сетку треугольников.
И наоборот, если игра ведется на углах шестиугольной сетки, на самом деле это треугольная сетка. Благодаря этому свойству равномерная сетка, состоящая из шестиугольников и треугольников, называется двойной сеткой.
Зачем использовать сетки треугольников
Треугольники обладают тремя удивительными свойствами:
- Они всегда плоские.
- они простые
- Их геометрия удобнее
Планарность
Если вы выберете любые три точки в трехмерном пространстве, вы всегда сможете провести через них плоскость. Таким образом, имея эти три точки, вы всегда можете нарисовать треугольник на поверхности этой плоскости. Это не всегда верно для многовершинных полигонов. Если вы возьмете четыре 3D-вершины, их сложно будет однозначно объединить в многоугольник с четырьмя вершинами. Многоугольники, страдающие от этой проблемы, называются неплоскими, и в компьютерной графике они могут стать серьезной помехой, поэтому почти вся графика в реальном времени преобразует все объекты в треугольники.
Хотя мы будем говорить о заполнении 2D-пространства, это свойство по-прежнему полезно для нас, когда мы хотим добавить карту высот. В треугольной сетке каждая вершина может быть на своей высоте, но в сетке проблем не будет. Если сделать то же самое с квадратной сеткой, то сразу же столкнемся с появлением неплоских вершин.

Sim City 2000 использует квадратную сетку и карту высот. Обратите внимание, что многие наклонные плитки разбиты на пары треугольников, потому что плитка неплоская.

Карта высот треугольной сетки. Со склонами проблем нет.
Простота
Математически вы можете видеть, что 3 меньше, чем 4 или 6. Это наименьшее количество вершин, которое может иметь многоугольник, поэтому треугольники — лучшая фигура для любого алгоритма, который масштабируется на основе количества точек или ребер.
Например, в моем туториале Marching Cubes я сказал, что для того, чтобы охватить все случаи в 2D, вам нужно создать разные тайлы. Это потому, что каждый из четырех углов имеет два варианта. У треугольников есть два варианта: взгляд вверх и взгляд вниз, поэтому для этих двух вариантов требуются разные плитки. Таким образом, в обоих случаях мы получаем 16 тайлов.

Обратите внимание, что для треугольников нет «противоречий».
Но это самый простой случай. Если разрешить возможность поворота плиток, то в случае с треугольниками вариантов меньше (4 против 6). А если нам нужно больше двух возможных значений в каждом углу (54 против 81 или 10 против 21 с поворотами/отскоками).
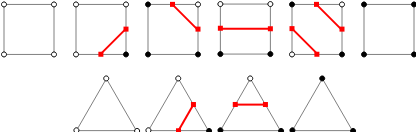
Вращающиеся пластины, необходимые для марша лодыжки
Кроме того, треугольники хороши для линейной интерполяции. Значения трех треугольников можно легко интерполировать с помощью барицентрических координат, тогда как для квадратов требуется более сложная билинейная интерполяция. Именно из-за этой разницы был придуман симплексный шум в качестве замены шума Перлина — они работают одинаково, но симплексный шум использует сетку треугольников (в случае 2D).
Геометрия лучше, чем у шестиугольников

При работе с шестиугольниками быстро понимаешь, что многие неудобства связаны с их гранями. Они не лежат по прямой! Это предотвращает разрыв сетки линейки. Нельзя построить большой шестиугольник из множества маленьких.
В следующей главе мы будем широко использовать прямые береговые линии, чтобы понять, как работают сетки.
Однако следует признать, что сетки треугольников имеют свои геометрические недостатки, в основном связанные с тем, как обращаться с треугольниками, смотрящими в разные стороны.
Как использовать сетки треугольников
Примечание. Этот учебник в основном посвящен концепциям и идеям, а не методам и коду. Если вас больше интересует реализация, изучите написанную мной эталонную реализацию.
Для начала следует сказать, что существует множество способов работы с треугольными сетками. В этой главе я опишу тот, который считаю лучшим — он прост для понимания и имеет простые выражения почти для всех действий, которые вам понадобятся для работы с треугольниками. Я буду описывать треугольники, расположенные рядами (треугольники, «смотрящие» вверх и вниз), но для мешей, повернутых на 90 градусов, это будет работать так же.
Хитрость заключается в том, чтобы думать о треугольной сетке как о трех наборах равномерно расположенных параллельных линий, перекрывающих друг друга:
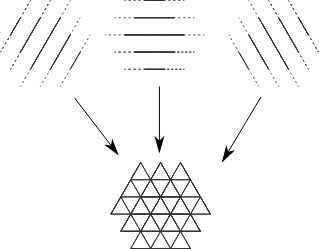
Пространство между каждой из этих параллельных линий называется полосами. Обозначим три направления полос как a, b и c, а сами полосы пронумеруем по порядку.
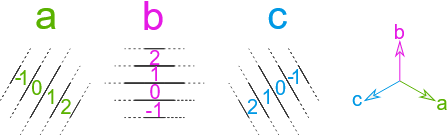
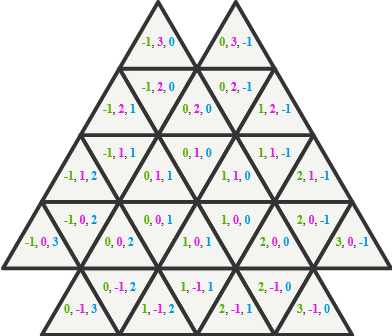
Тогда координатами треугольника будут три целых числа a, b, c, которые определяют полосы движения, в которых находится треугольник. Все очень просто!

Вам, наверное, интересно, почему мы используем три числа для описания ячейки в 2D-сетке. Просто нам так удобнее работать. Если вы попытаетесь использовать двухчисловую систему координат, вам придется добавить больше исключений для четных и нечетных координат или других аспектов. Аналогичный прием используется при работе с шестиугольными сетками, см. эту статью о «кубических» координатах шестиугольных сеток. С другой стороны, третья координата почти избыточна — в этой системе сумма a + b + c всегда равна либо 1, либо 2. Так что мы можем просто хранить a, b и c в дополнительной булевой переменной.
Стоит отметить, что в такой системе нет треугольника с координатами (0, 0, 0). Я пронумеровал бары так, что начало представляет собой вершину, окруженную шестью треугольниками в барах 0 и 1. Когда бары пронумерованы по-разному, система работает одинаково.
Соседи
Переходя от одного треугольника к другому, мы пересекаем одну из линий, разделяющих полосы. Я создал систему так, что когда мы выходим из треугольника вершиной вниз, мы прибавляем единицу к координате. А начиная с треугольника вершиной вверх, отнимаем единицу.

Центр треугольника
Поскольку переход к соседнему треугольнику — это всегда шаг заданного размера по одной из трех полос, данный треугольник можно найти, просто просуммировав все шаги, сделанные в трех направлениях.
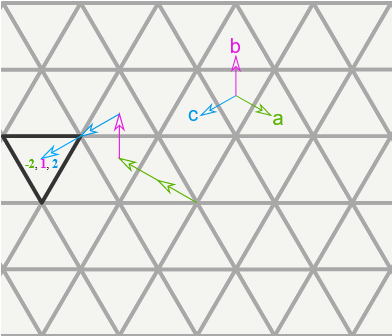
Расстояние между треугольниками
Поскольку каждый шаг изменяет координату на единицу, формула расстояния — это просто разность каждой координаты.
В следующей статье я рассмотрю альтернативную функцию расстояния.
В каком треугольнике находится точка
Чтобы найти треугольник, содержащий точку, вам просто нужно идентифицировать три полосы, в которых находится треугольник. Это можно сделать, измерив расстояние перпендикулярно полосе от начала, что легко сделать с помощью скалярного произведения с последующим усечением до целого числа.
ceil округляет число до ближайшего целого числа, а floor округляет его в меньшую сторону. Нельзя просто закруглять все три полоски в одном направлении, иначе будут сложности, например, с точкой с координатой (0, 0), которая находится на углу шести разных треугольников.
Другие операции
С сеткой можно выполнять многие другие операции, такие как измерение расстояний, рисование линий и выполнение поворотов.Все это подробно описано в моей эталонной реализации на github.
Вы можете сравнить это с реализацией шестиугольной сетки.С треугольниками намного проще работать, чем с шестиугольниками, поэтому я реализовал множество операций с шестиугольниками, сначала выполнив операцию эквивалентного треугольника, а затем преобразовав их в шестиугольники.
Надеюсь, я убедил вас, что сетки — недооцененный инструмент.
Процедурная генерация мешей Tessera
Дополнительные материалы
Статья RedBlobGaming о сетках по-прежнему остается лучшим источником знаний о сетках.Слышал, что он работает над обновленной версией.
Также могу порекомендовать статью Джастина Помбрио о преобразовании пикселей в шестиугольники, из которой я узнал, насколько удобно работает система треугольников и как она соотносится с шестиугольными сетками.







